Pernahkah anda (khususnya mahasiswa matematika atau mereka yang pernah ikut olimpiade matematika) disuruh membuktikan suatu teorema matematika? PASTINYA! Kalo gak pernah saya ragu kalau anda adalah mahasiswa matematika :D
Ya, melakukan pembuktian adalah suatu hal yang rutin dilakukan oleh para mahasiswa matematika pada umumnya, karena (menurut saya) hal itu akan melatih pola berfikir sebagai calon matematikawan. Bukan matematikawan sejati yang tidak pernah sekalipun membuktikan satu teorema pun.
By the way, pertama saya akan menjelaskan apa itu teorema. Secara sederhana teorema adalah suatu pernyataan yang harus dibuktikan kebenarannya/dapat ditunjukkan kebenarannya. Berbeda dengan aksioma yang tidak perlu pembuktian sama sekali. Dalam hirarki pembuktian matematika, teorema berada di bawah aksioma dan postulat posisinya atau lebih rendah tingkatannya dibanding aksioma dan postulat. Cara-cara pembuktian teoerma sangat beragam, bisa bukti langsung, bukti tak-langsung atau reductio ad absurdum, bukti dengan kasus dan lain sebagainya. Jenis-jenis pembuktian ini akan dijelaskan pada postingan berikutnya.
Sekarang kita fokus kembali mengenai apa itu bukti formal dan bukti informal. Kebanyakan mahasiswa matematika tidak terlalu mengenal apa itu bukti formal dan apa itu bukti informal. Maka dari itu saya akan menjelaskan apa itu bukti formal terlebih dahulu.
Bukti Formal
Bukti formal secara sederhana merupakan suatu langkah pembuktian berdasarkan logika dari himpunan premis dan aksioma. Artinya pembuktian formal adalah pembuktian yang mengikuti aturan inferensi. Secara sederhana, aturan inferensi tampak seperti ini:
Dimana p merupakan premis-premis berhingga dan q merupakan konklusi atau kesimpulan. Perlu diketahui bahwa suatu kesimpulan yang benar diperoleh berdasarkan premis-premis yang benar. Hal ini dapat dilihat dari operasi biner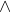 
. Jika salah satu premis salah maka nilai kebenaran dari 
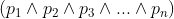juga salah sehingga kesimpulan yang diperoleh juga salah. Hasil dari pembuktian yang mengikuti aturan inferensi haruslah berupa tautologi, artinya harus selalu bernilai benar.
Sekarang kembali fokus pada bukti formal. Bukti formal pada dasarnya berbentuk langkah-langkah logika, misalnya saya memiliki pernyataan A dan B dan ingin membuktikan bahwa kesimpulannya adalah TIDAK A, maka:
Pada pembuktian formal biasanya menggunakan komputer untuk mengklarifikasi kebenaran suatu teorema. Banyak sekali program pembuktian matematika yang disebut sebagai Automated Theorem Prover (Pembukti Teorema Otomatis) seperti Isabelle, HOL, Coq, Mizar dan lain sebagainya. Kali ini saya akan menunjukkan salah satu bukti formal mengenai pembuktian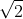 
adalah bilangan irasional menggunakan Mizar Ver.6.1.11 - 3.33.722:
- Sketsa Pembuktian Formal: Layout Informal
PROOF assume sqrt 2 is rational; consider a, b such that
4_3_1: a^2 = 2 * b^2
and a,b are_relative_prime; a^2 is even; consider c such that a = 2 * c;
4 * c^2 = 2* b^2; 2 * c^2 = b^2; b is even; thus contradiction; END;
- Sketsa Pembuktian Formal: Layout Formal
proof
assume sqrt 2 is rational;
consider a,b such that
4_3_1: a^2 = 2*b^2 and
a,b are_relative_prime;
a^2 is even; *4
a is even; *4
consider c such that a = 2*c; *4
4*c^2 = 2*b^2; *4
2*c^2 = b^2; *4
b is even; *4
thus contradiction; *1
end;
- Bukti Formal
proof
assume sqrt 2 is rational;
then consider a,b such that
A1: b <> 0 and
A2: sqrt 2 = a/b and
A3: a,b are_relative_prime by Def1;
A4: b^2 <> 0 by A1,SQUARE_1:73;
2 = (a/b)^2 by A2,SQUARE_1:def 4
.= a^2/b^2 by SQUARE_1:69;
then
4_3_1: a^2 = 2*b^2 by A4,REAL_1:43;
a^2 is even by 4_3_1,ABIAN:def 1;
then
A5: a is even by PYTHTRIP:2;
then consider c such that
A6: a = 2*c by ABIAN:def 1;
A7: 4*c^2 = (2*2)*c^2
.= 2^2*c^2 by SQUARE_1:def 3
.= 2*b^2 by A6,4_3_1,SQUARE_1:68;
2*(2*c^2) = (2*2)*c^2 by AXIOMS:16
.= 2*b^2 by A7;
then 2*c^2 = b^2 by REAL_1:9;
then b^2 is even by ABIAN:def 1;
then b is even by PYTHTRIP:2;
then 2 divides a & 2 divides b by A5,Def2;
then
A8: 2 divides a gcd b by INT_2:33;
a gcd b = 1 by A3,INT_2:def 4;
hence contradiction by A8,INT_2:17;
end;
Bukti Informal
Setelah mengetahui apa yang dimaksud dengan bukti formal, apakah anda sudah bisa menebak seperti apa bukti informal? Ya! Bukti informal adalah pembuktian dengan kata-kata sehari-hari seperti "Akan gue buktiin..." atau "Dengan semau gue..." atau "Nah lo bisa liat bahwa terjadi kontradiksi di sini dan di situ". #PLAK #PLAK #WADEZIG! Sori-sori becanda :3 Sebenarnya yang dimaksud dengan bukti informal adalah suatu bentuk pembuktian yang bertujuan untuk menyimpulkan pernyataan baru berdasarkan pernyataan yang sudah diketahui sebelumnya. Bedanya pada pembuktian informal lebih cenderung kepada penulisan bukti dalam bentuk paragraf dibanding hanya bentuk-bentuk logika. Pembuktian dengan bukti informal sangat sering digunakan pada umumnya bagi mereka yang berkecimpung di dunia matematika. Dari bukti informal, seorang ahli matematika/ahli komputer dapat mengkonstruksi bukti formal untuk dibuktikan kebenarannya menggunakan komputer, walaupun untuk mengkonstruksi bukti informal ke bukti formal pada prinsipnya membutuhkan waktu yang cukup lama melelahkan.
Berikut merupakan salah satu bukti informal mengenai pembuktian 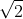adalah bilangan irasional oleh G.H. Hardy dan E.M. Wright dalam buku yang berjudul An Introduction to the Theory of Numbers. 4th edition.
Teorema 43 (Teorema Phytagoras). 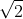adalah bilangan irasional.
Bentuk pembuktian ini adalah sebagai berikut. Jika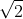 adalah rasional, maka persamaan:
Bentuk pembuktian ini adalah sebagai berikut. Jika
memiliki solusi dalam bilangan bulat a, b dengan (a, b) = 1. Karena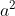 
genap, maka a juga bilangan genap. Jika a = 2c, maka 
, 
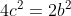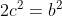, dan b juga genap, kontradiksi dengan hipotesis bahwa (a, b) = 1.
Sumber: Nine Formal Proof Sketches oleh Freek Wiedijk, University of Nijmegen
0 komentar:
Posting Komentar