[Darimana Asalnya?] $e^{i\pi}=-1$

Sumber: upload.wikimedia.org

Suatu ketika Michael Atiyah, seorang guru besar matematika dari University of Edinburgh yang sangat terkenal di Inggris, melakukan penelitian bersama Semir Zeki, seorang ahli neurobiologi dari University College London, dan kolaborator lainnya, dengan judul The Experience of Mathematical Beauty and Its Neural Correlates (Pengalaman akan Keindahan Matematika dan Korelasi Neural-nya <- kira-kira ini terjemahan versi saya, maaf kalo ada salah hehehe :D). Penelitian itu bertujuan untuk meneliti apakah otak dapat merespon keindahan dari matematika dan apakah berada pada bagian dari otak yang sama seperti saat kita merespon keindahan suatu musik, atau puisi atau lukisan. Penelitian ini dilakukan dengan cara menunjukkan beberapa persamaan matematika ketika otak para responden direkam menggunakan MRI (Magnetic Resonance Imaging). Kesimpulannya adalah: ya! Tapi yang menarik dari penelitian ini adalah ada suatu persamaan matematika yang dianggap paling indah oleh beberapa responden, yaitu $$e^{i\pi}=-1$$Mungkin sebagian pembaca bertanya-tanya mengapa persamaan di atas dianggap yang paling indah menurut para responden, termasuk saya sendiri juga menganggapnya demikian. Nah, pada kali ini saya akan menjelaskan mengenai darimana asal-usul dari persamaan di atas.

Pada rumus di atas, terdapat 3 konstanta matematika, yaitu $\pi$ yang merupakan bilangan irasional yang memiliki desimal tidak terbatas, yaitu $\pi=3.1415926...$ lalu $i$ merupakan bilangan imajiner yang memiliki nilai $i=\sqrt{-1}$ dan yang terakhir $e$, disebut juga bilangan Euler, yang merupakan bilangan irasional bernilai $e=2.718281...$. Jadi, bagaimana caranya kombinasi dari ketiga bilangan ini menghasilkan bilangan negatif?

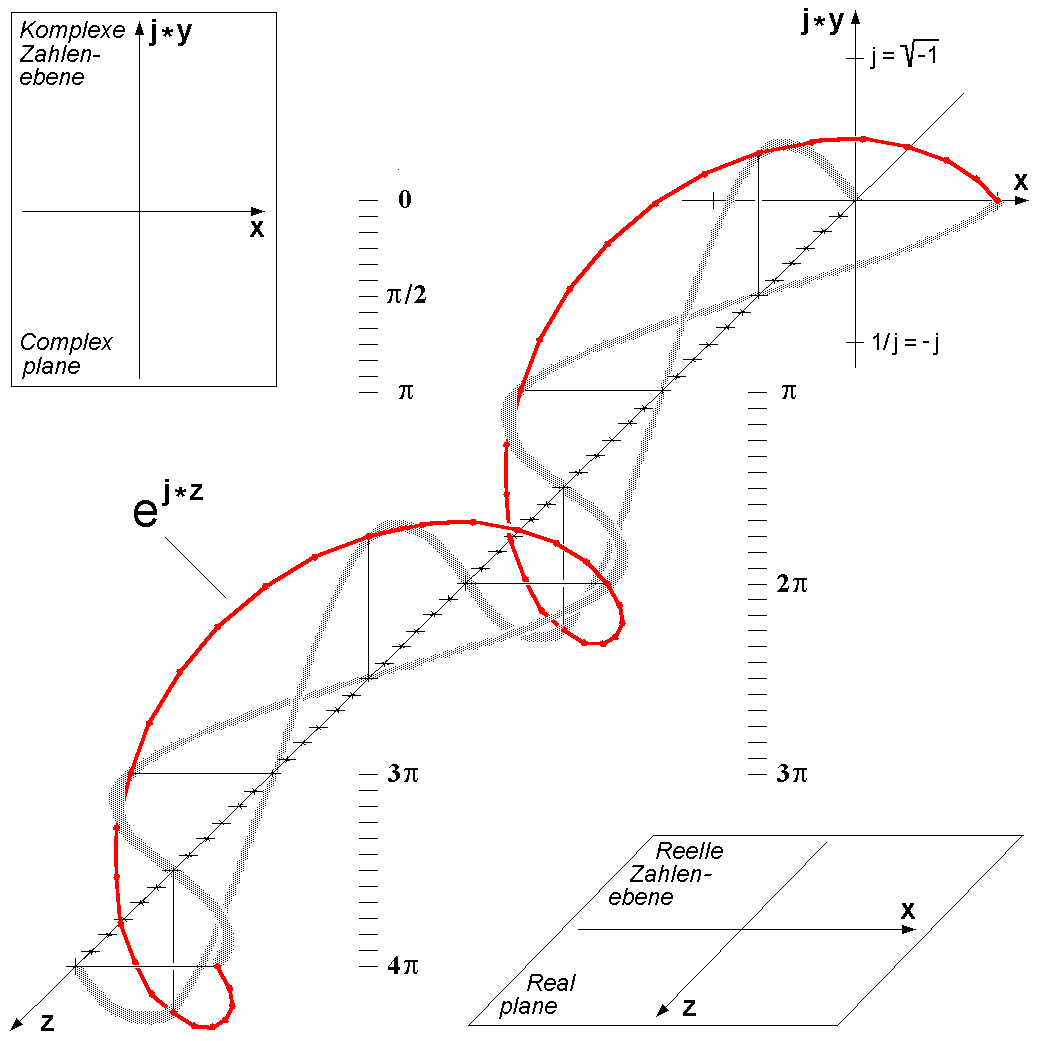
Pertama, kita harus tahu dulu bahwa $$e^{x}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+...$$Bentuk di atas biasa disebut sebagai deret pangkat dari $e$. Selain itu kita juga perlu tahu bahwa $$\sin{x}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...$$dan $$\cos{x}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...$$Pertama, kita tulis deret pangkat dari $e$ sebagai $$e^{ix}=1+ix+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+...$$Dengan mengingat bahwa $i=\sqrt{-1}$, $i^2=-1$, $i^3=-i$, $i^4=1$ dan seterusnya, maka deret pangkat di atas bisa diubah menjadi $$e^{ix}=1+ix-\frac{x^2}{2!}-\frac{(ix)^3}{3!}+\frac{(x)^4}{4!}+...$$dan dengan 'sedikit' mengatur persamaan di atas dapat diperoleh $$e^{ix}=1-\frac{x^2}{2!}+\frac{x^4}{4!}+...+ix-\frac{ix^3}{3!}+\frac{ix^5}{5!}-...$$atau $$e^{ix}=1-\frac{x^2}{2!}+\frac{x^4}{4!}+...+i(x-\frac{x^3}{3!}+\frac{x^5}{5!}-...)$$Perlu diingat bahwa

$$e^{ix}=\underset{\cos{x}}{\underbrace{1-\frac{x^2}{2!}+\frac{x^4}{4!}}}+...+i\underset{\sin{x}}{\underbrace{(x-\frac{x^3}{3!}+\frac{x^5}{5!}-...)}}$$Sehingga bentuk di atas dapat diubah menjadi $$e^{ix}=\cos{x}+i\sin{x}$$Selanjutnya dengan mengganti variabel $x$ dengan $\pi$, diperoleh $$e^{i\pi}=\cos{\pi}+i\sin{\pi}$$Ingat bahwa $\pi=180\unicode{xb0}$, sehingga $\cos{\pi}=-1$ dan $\sin{\pi}=0$, sehingga diperoleh $$e^{i\pi}=-1$$Wow, ternyata 'cukup' menggunakan beberapa persamaan untuk membuktikan persamaan yang indah ini :) Oh ya seingat penulis ada cara lain yang dapat dipakai untuk membuktikan persamaan ini, bagi yang tahu silahkan berbagi di bagian komentar. Cukup sekian postingan hari ini, semoga penulis masih punya nyawa untuk menulis hehehe ~_~

Sumber:

1. Michael Atiyah's Imaginative State of Mind - https://www.quantamagazine.org/20160303-michael-atiyahs-mathematical-dreams/

Read More

[Dari mana asalnya?] $\sin^2(x)+\cos^2(x)=1$

Bagi yang pernah merasakan 'kejamnya' subjek trigonometri pasti setidaknya pernah melihat salah satu identitas trigonometri paling mudah diingat ini:
$$\sin^2(x)+\cos^2(x)=1$$
Namun adakah yang pernah memikirkan dari mana asalnya rumus ini? Mungkin karena kebanyakan mikirin gebetan PR yang banyak atau mantan tidak begitu penting sehingga tidak ada waktu untuk mikirin darimana asalnya identitas trigonometri ini bisa ada :)
Nah, maka dari itu saya akan memberikan penjelasan darimana rumus diatas berasal. Sebelum itu kita ingat dulu definisi dari sinus dan cosinus sebagai perbandingan dari sisi-sisi segitiga siku-siku.

Segitiga siku-siku. Sumber: upload.wikimedia.org

Sinus atau biasa ditulis sebagai $\sin(\alpha)$ merupakan perbandingan antara sisi dihadapan sudut yang disimbolkan dengan $a$, dengan sisi miring atau hipotenusa yang disimbolkan dengan $h$, sehingga
$$\sin(\alpha) = \frac{a}{h}$$
Cosinus atau biasa ditulis sebagai $\cos(\alpha)$ merupakan perbandingan antara sisi disamping sudut yang disimbolkan dengan $b$, dengan sisi miring atau hipotenusa, sehingga:
$$\cos(\alpha)=\frac{b}{h}$$
Sekarang, kita akan buktikan bahwa
$$\sin^2(x)+\cos^2(x)=1$$
Jika $\sin(\alpha) = \frac{a}{h}$, maka
$$\sin^2(\alpha) =( \frac{a}{h})^=\frac{a^2}{h^2}$$
sedangkan jika $\cos(\alpha)=\frac{b}{h}$, maka
$$\cos^2(\alpha)=(\frac{b}{h})^2=\frac{b^2}{h^2}$$
sehingga
$$\sin^2(\alpha)+\cos^2(\alpha)=\frac{a^2}{h^2}+\frac{b^2}{h^2}$$
$$=\frac{a^2+b^2}{h^2}$$
Perhatikan segitiga siku-siku diatas! Jika kita masih ingat mengenai rumus Phytagoras, kita dapat mengetahui bahwa
$$h^2=a^2+b^2$$
sehingga
$$\frac{a^2+b^2}{h^2}=\frac{h^2}{h^2}=1$$
Maka dari itu diperoleh:
$$\sin^2(\alpha)+\cos^2(\alpha)=1$$

Ternyata tidak sulit untuk membuktikan atau mencari tahu dari mana asalnya identitas trigonometri yang satu ini. Cukup dengan menggunakan definisi dari sinus dan cosinus.
Cukup sampai disini postingan saya, semoga bermanfaat :)

Read More

Gila dengan Istilah

Saya sudah memulai penelitian saya mengenai Geometri Nonkomutatif, and It's crazy. Maksud saya, banyak sekali istilah fisika yang harus saya hapal dan mengerti. Mulai dari kata invarian, ruang fase, aljabar observabel, prosedur akses, bahkan yang sempat membuat saya bingung adalah swakeadaan. Kata apa ini? Saya mencari di situs kbbi.web.id dan.... tidak ketemu

See? Gak ada penjelasannya

Berhubung saya memang tidak punya KBBI edisi terbaru, saya mau tidak mau mencarinya di Google, dan akhirnya saya menemukan artinya, yaitu keadaan eigen. Apa lagi itu keadaan eigen? Saya belum mempelajarinya terlalu dalam. Saya banyak teralihkan dengan kesibukan saya bekerja ditambah dengan keinginan saya untuk bisa berbahasa Jerman. Mau gak mau saya harus mencoba mengatur ulang waktu saya mulai minggu depan.

BTW saya sudah menentukan kemana saya harus melanjutkan kuliah saya andaikan saya mendapat beasiswa LPDP, yaitu ke Georg-August-Universität Göttingen. Saya memilih disana karena selain menurut saya lebih mudah belajar bahasa Jerman dibanding bahasa Danish (sempat belajar sedikit karena dulu ingin ke Copenhagen), juga disana terdapat grup riset bidang geometri nonkomutatif. Selain itu saya dari dulu ingin sekali bisa kuliah ke Eropa, benua yang sangat indah untuk studi lanjut.

Georg-August-Universität Göttingen

Mungkin untuk postingan kali ini tidak begitu banyak yang bisa saya bagi kepada pembaca, semoga minggu depan bisa menulis hal yang lebih bermanfaat. Sie nächste Woche :)

Read More